Data 8 学习笔记(四)

数据科学简直就是统计学披着计算机的外皮。
——我

Testing Hypothesis 假设检验

这里我们以孟德尔的豌豆花形状实验为例，孟德尔的模型是，对于每一株豌豆有75%其有紫色花，25%其为白花，其颜色和其他植株独立。

Step 1: The Hypothesis 假设

The Null hypothesis 零(原)假设：零假设认为所有数据都是在明确指定的条件下生成的，如果数据结果和零假设不同，那只可能是因为偶然性。

但是我们最关心的是，在实际应用中，零假设是我们研究者提出的，用来模拟数据的假设。

对于孟德尔模型来说，零假设就是其模型是正确的，即每株豌豆有75%是紫色花，25%是白色花，且互相独立。

The Alternative Hypothesis 备选假设：备选假设站在零假设的对立面，它说明除了概率以外的其他因素导致了结果和零假设相悖。

对于孟德尔模型来说，备选假设很简单，就是孟德尔模型不正确。这里我们并不说明理由和影响因素。

Step 2: The Test Statistic 检验统计量

为了在这两个假设之间作出决策，我们必须选择一个统计量作为我们决策的依据。 这被称为检验统计量 Test Statistic。

TVD(Total Variation Distance) 总变差距离：量化两个概率分布的距离

$TVD(P, Q) = \frac{1}{2} \sum_x|P(x) - Q(x)|$

即两个概率分布的TVD是每个事件概率差的绝对值的和除以二

TVD的值在0到1之间：

  • TVD = 0 表示两个分布完全相同
  • TVD = 1 表示两个分布完全不重叠

以孟德尔的实验结果为例，929株豌豆中有705株有紫色花，我们选择计算随机抽样结果和模型的相关性，于是我们计算这两个分布的TVD。为了更好的观察数据我们把结果转换成百分比。

Observed Value of the Test Statistic 检测统计量的观测值：这里随机抽样得到的705/929是检测统计量的观测值，该数据并非我们通过模拟得到的。

TVD = 0.5 * (abs(100 * 705/929 - 75) + abs(100 * 224/929 - 25)) TVD 的结果是 0.8880516684607045。

Step 3：The Distribution of the Test Statistic, Under the Null Hypothesis 在原假设下检测统计量的概率分布

为了搞清楚原假设的模型预测的数据是什么样的，我们需要知道如果原假设是正确的，我们应该得到的检验统计量应该是怎样的。 于是我们需要把原假设为正确作为前提来模拟，通过抽样过程的大量重复和统计量的经验分布来近似检验统计量的概率分布。。

  • 对于每个植株，紫花的概率是0.75
  • 样本大小是929
  • 每次模拟我们生成929次，记录其中紫花的比例还有其与原假设(75%)的距离， 也就是|紫花的百分比 - 75|
  • 重复模拟

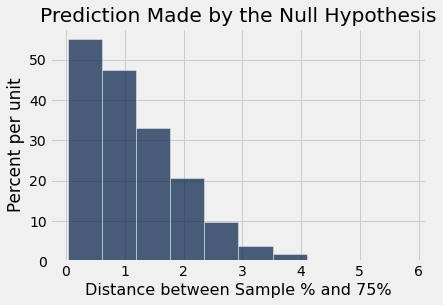
结果可视化后如图
result
我们可以发现，大部分的数据在0到1的区间内，也就是模拟数据和理想状况(75%)的距离大多数在0到1之间。

接下来我们要比较我们根据原假设的预测和莫德尔的实际观察数据。

Step 4. The Conclusion of the Test 下结论

原假设和备选假设之间的选择，取决于Step 2 和 3 的结果之间的比较：检验统计量的观察值以及由原假设预测的概率分布。

如果二者一致consistent，则观察到的检验统计量与原假设的预测一致。 换句话说，这个检验并不偏向备选假设；数据更加支持原假设。

但如果两者不一致，就像我们阿拉米达县陪审团的例子那样，那么数据就不支持原假设。 这就是为什么我们得出结论，陪审团不是随机挑选的。 几率之外的东西影响了他们的构成。

如果数据不支持原假设，我们说检验拒绝reject了原假设。

我们从Step 2得知，孟德尔的数据检测统计量的观测值是大约0.89，这和我们在Step 3里面的结果相吻合，也就是说孟德尔的模型，也就是原假设相比于备选假设更正确。

补充

判断检测统计量和预测是否一致的指标目前很不明确，所以我们需要用更系统的方式去决定什么时候我们认为两者consistent一致。

Significance and p-value 显著性和p值

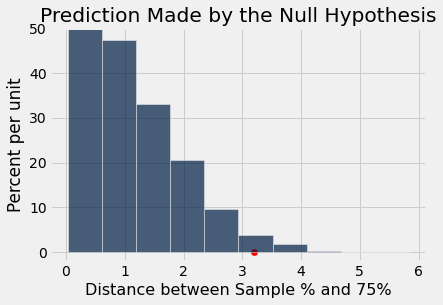
孟德尔的数据的和原假设预测的TVD是0.89，但是如果我们的数据和原假设的TVD是3.2呢？我们怎么判断原假设和备选假设哪个更正确呢？

result
我们可以看见，3.2的TVD位于红点所在的位置。 惯例上，我们习惯于通过尾部tail来判断，也就是从红点向偏向于备选假设的方向，在这里是右方。如果tail的面积(在直方图里面积就是比例)过小，我们就可以说观察到的数据和符合原假设的预测相去甚远。

通过计算，我们可以得到有2.4%的在原假设下的模拟数据的TVD大于3.2，这个概率很小了，如果原假设是正确的话我们的数据应该有97.6%概率比3.2小。这时我们就需要引入convention惯例了。

p-value p值

显著性 (Significance) 用来评估观察到的测试统计量有多不寻常，即在原假设成立的情况下，这个统计量出现的概率有多低，这个值我们称为p-value p值，也就是我们上面所计算的2.4%。

Definition: The p-value of a test is the chance, based on the model in the null hypothesis, that the test statistic will be equal to the observed value in the sample or even further in the direction that supports the alternative.

Significance level

在实际运用中我们会设置一个阙值cutoffs(显著性水平) $\alpha$： conventional cutoffs一般来说，我们认为5%是一个方便的极限，也就是

  • $p <= \alpha$的时候结果统计显著，即有足够证据拒绝原假设。
  • $p > \alpha$，则无法拒绝原假设。

统计学上显著性水平 $\alpha$ 是第一类错误(Type I error)的容忍度：

第一类错误：错误地拒绝了原本真实的原假设。 比如 $\alpha = 0.05$，就代表即便原假设是真的，仍有 5% 的可能性我们会误判为拒绝。

第二类错误：备择假设 (Alternative Hypothesis) 为真，但错误地没有拒绝原假设。 Data8暂时不覆盖计算Type Ⅱ error的概率计算。

Data Snooping and p-Hacking 数据窥探

咱们在高中物理化学生物实验就做过类似的事情了~在分析前或假设检验之前，反复探索数据、试图找到看似显著的关系，或者为了使p值小于等于0.05改变分析方法强行得到结果。

Needless to say, 这样会导致很多问题

  • 结果可复现性极低
  • 增加假阳性 false positive
  • 结果不具有统计效度

为了academic integrity 我们一定要事前定义好假设和方法，不去反复调整，统计显著性才可信，否则结果的p<=0.05可能只是数据随机波动的幻觉。

Project 2 Part 1

project1很基础很简单，但是project 2 开始涉及一些系统的统计学术语了，有些在textbook里没进行阐述。Part 2 的内容包括教科书第12章的内容，下一个笔记会涵盖。

置信区间及其计算

置信区间 Confidence Interval CI: 置信区间是指由样本统计量所构造的总体参数的估计区间

置信区间是基于样本数据，对总体参数（例如总体均值）的一种区间估计。
常用的置信水平（Confidence Level）有 95%、99% 等。
例如，95% 置信区间意味着：

如果重复抽样并计算置信区间，多次后约95%的区间会包含真实总体参数。

线性插值： 如果百分位数对应的位置是浮点数，取它相邻的两个点，按距离比例计算加权平均。

也就是对于第2和第3个数据加权平均0.5。但是np使用np.percentile()就自动进行插值了，很方便
本节我们只学习bootstrap方法取置信区间，具体代码实现如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def bootstrap_ci(data, statistic_func, num_samples=5000, ci=95):
    """
    计算给定数据和统计量的 Bootstrap 置信区间
    data: 原始样本数据 (np array)
    statistic_func: 统计量函数 (如 np.mean, np.median)
    num_samples: 重采样次数
    ci: 置信水平 (百分数)
    """
    boot_stats = make_array()
    for _ in range(num_samples):
        resample = np.random.choice(data, size=len(data), replace=True)
        stat = statistic_func(resample)
        boot_stats = np.append(boot_stats, stat)
    
    lower = np.percentile(boot_stats, (100 - ci) / 2)
    upper = np.percentile(boot_stats, 100 - (100 - ci) / 2)
    return lower, upper

Reference

Data 8 Text book: Inferential Thinking chapter 11