Data 8 学习笔记(三)

Numpy random.choice()

有时我们需要从集合里随机选取一个值，这时就可以用np.choice()，具体语法是：

1
2
3
4
5
6
#随机选取一个值
random_choice = np.choice(array_name)
#多次随机选取
random_choices = np.choice(array_name, frequency)
#模拟掷骰子三次
dice_rolls = np.choice(np.arange(1,7), 3)

模拟 simulation - 以原神抽卡为例

Step 1: What to simulate?

我们想要模拟每次抽到五星物品的预计抽数。
每一次抽卡只会有两个结果：

  • 抽到五星物品
  • 没抽到五星物品

Step 2: Simulating one play.

接下来我们模拟一次抽卡的结果。目前我们只考虑五星，不考虑四星插队的情况，也不考虑up角色的情况：

在前73抽，每次出现五星物品的概率为0.6%。 从第74抽开始，每次增加6%的概率直至第90抽到达100%。

我们定义一个函数calc_chance来计算每一抽出五星的概率，传入参数pity为目前抽数：

1
2
3
4
5
6
7
def calc_chance(pity):
    if pity < 74:
        return 0.006
    elif pity < 90:
        return 0.006 + 0.06 * (pity - 74)
    else:
        return 1.0

那么对于一次模拟，我们定义函数one_simulation获得出五星时的抽数：

1
2
3
4
5
6
def one_simulation():
    pity = 0
    while True:
        pity += 1
        if np.random.random() < calc_chance(pity):
            return pity

Step 3: Number of repetition

模拟次数由我们决定，次数越多结果越可靠，但是耗时越长。 这里我们仅仅模拟10000次试试：

  • 也就是说我们要模拟抽到五星物品的抽卡数10000次

Step 4: Simulating Multiple Values

1
2
3
4
5
6
7
8
9
num_of_repetition = 10000
res = []
for i in range(num_of_repetition):
    res.append(one_simulation())
res = np.array(res)
simulation_result = Table().with_columns(
    "Repetition", np.arange(1, num_of_repetition + 1),
    "Count", res
    )

在simulation_result里我们获得了10000次模拟组成的Table。 接下来我们可以用直方图直观的查看数据分布, 并用np.mean查看出五星的平均抽数：

1
2
simulation_result.hist("Count", bins=np.arange(1, 91, 1))
np.mean(res) #在jupiter notebook里会自动打印每个cell的最后一行代码

结果如图：
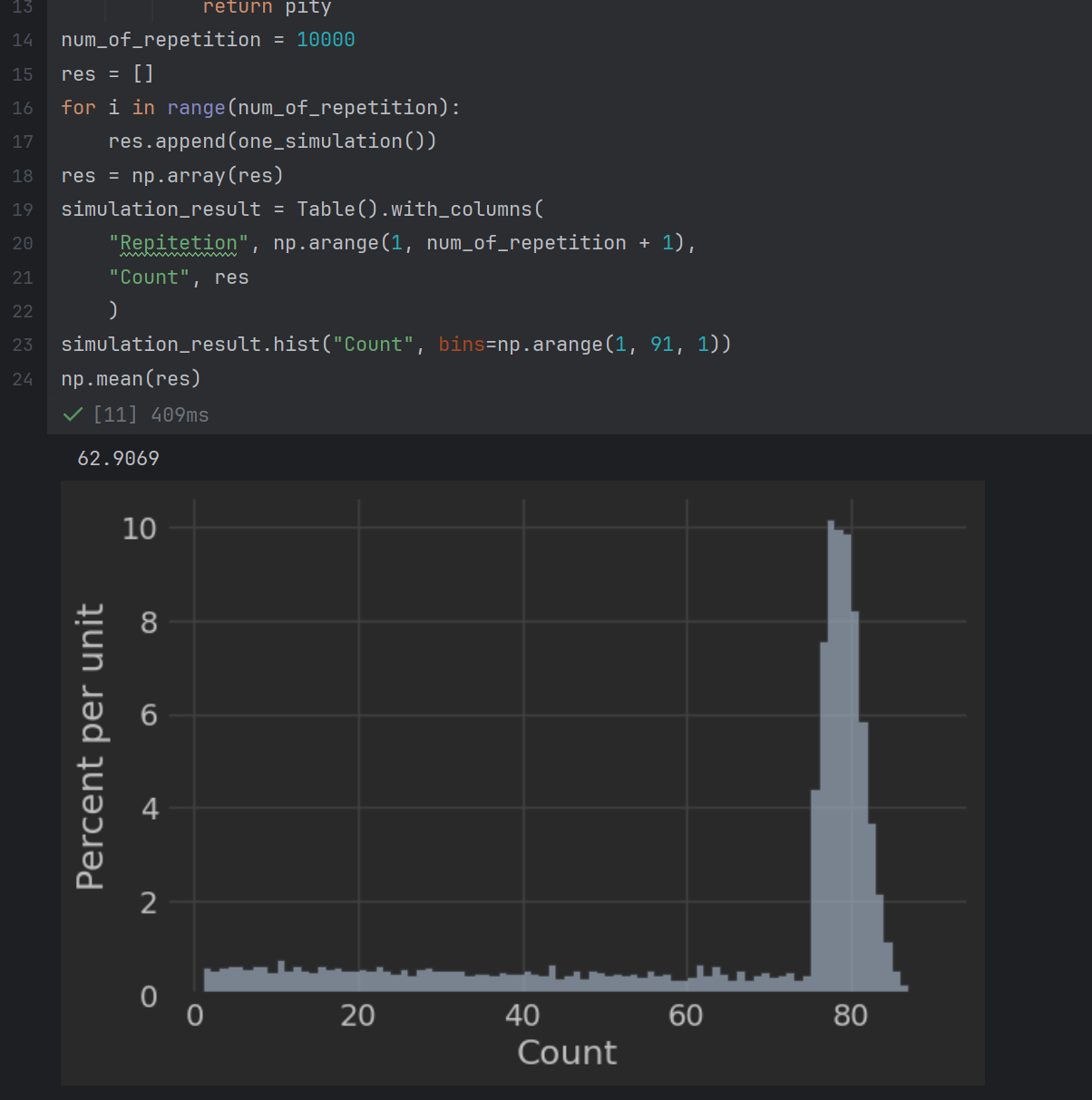
result
所以说我们可以得出结论，原神出金的平均抽数为大约63抽，但是大部分人会在74抽以后出金。
当然我们也可以用np.median()获得中位数数据。

Monty Hall Problem 三门问题

经典的统计学问题，国内高中数学应该早有接触的。我们也可以用模拟来得出大概结论。具体情景可以参考三门问题。有三道门，背后分别由一辆汽车两个山羊，参与者从中选择一道门，然后主持人从剩余的两道门里指出背后有山羊的一道门，并询问参与者是否选择更换自己的选择。

有一种反直觉但是符合逻辑的方式理解这个问题：

  • 从三道门里任选一个门背后有汽车的概率是1/3
  • 那么选择一道门以后，剩余两道门里有汽车的概率为2/3
  • 当得知剩余两道门的一道门背后有山羊后，最后的一道门里有车的概率还是2/3
  • 所以如果选择换门，获得汽车的概率为2/3，不换门的话概率仍然是1/3

通过我们提到的模拟，我们也能得出一样的结论，具体可以查看data8教科书第9章第4节。

Discrete Distribution 离散分布

Monash MAT1830离散数学里有提到几种离散分布：

Bernoulli Distribution

  • Definition: A distribution with only two outcomes: success ($1$) or failure ($0$).
  • Parameter:
    • $p$: probability of success
  • Support: $x \in {0, 1}$
  • PMF (Probability Mass Function):
    $$
    P(X = x) = p^x (1 - p)^{1 - x}
    $$
  • Mean: $\mu = p$
  • Variance: $\sigma^2 = p(1 - p)$

Binomial Distribution

  • Definition: Number of successes in $n$ independent Bernoulli trials.
  • Parameters:
    • $n$: number of trials
    • $p$: probability of success
  • Support: $x \in {0, 1, …, n}$
  • PMF:
    $$
    P(X = x) = \binom{n}{x} p^x (1 - p)^{n - x}
    $$
  • Mean: $\mu = np$
  • Variance: $\sigma^2 = np(1 - p)$

Geometric Distribution

  • Definition: Number of trials until the first success.
  • Parameter:
    • $p$: probability of success per trial
  • Support: $x \in {1, 2, 3, \dots}$
  • PMF:
    $$
    P(X = x) = (1 - p)^{x - 1} p
    $$
  • Mean: $\mu = \frac{1}{p}$
  • Variance: $\sigma^2 = \frac{1 - p}{p^2}$

Poisson Distribution

  • Definition: Models the number of events in a fixed interval of time or space.
  • Parameter:
    • $\lambda$: average rate of occurrence
  • Support: $x \in {0, 1, 2, \dots}$
  • PMF:
    $$
    P(X = x) = \frac{e^{-\lambda} \lambda^x}{x!}
    $$
  • Mean: $\mu = \lambda$
  • Variance: $\sigma^2 = \lambda$

Discrete Uniform Distribution

  • Definition: All outcomes are equally likely.
  • Parameter:
    • $a, b$: integers, where $a \leq x \leq b$
  • Support: $x \in {a, a+1, \dots, b}$
  • PMF:
    $$
    P(X = x) = \frac{1}{b - a + 1}
    $$
  • Mean:
    $$
    \mu = \frac{a + b}{2}
    $$
  • Variance:
    $$
    \sigma^2 = \frac{(b - a + 1)^2 - 1}{12}
    $$

小总结

不需要记公式，只需要知道什么情况下用哪一种分布即可：

  • 伯努利分布：单次试验，只有两种可能结果（成功/失败）
    例：抛一次硬币

  • 二项分布：重复 $n$ 次独立伯努利试验，统计成功次数
    例：抛 $n$ 次硬币，看出现正面的次数

  • 几何分布：独立重复试验直到首次成功，记录试验次数
    例：没有保底的抽卡，出金需要几次(之前做的原神抽卡模拟就是几何分布，但是概率不恒定)

  • 泊松分布：单位时间或空间内，事件发生的次数
    例：一分钟内收到的电话数量，或连续掷骰子 100 次，6 出现的次数

  • 离散均匀分布：每个可能结果的概率完全相等
    例：标准六面骰任意一次掷出的点数

抽样 Sampling

于表格Table而言，抽样的个体就是一行数据row

确定性样本 Deterministic Samples

其实我们之前已经取过确定性样本了，我们使用的Table.take()可以取出给定的行，而Table.where()可以根据一定条件取出所需要的行，这些都是确定性样本，因为它们都不涉及任何概率计算，是基于给定的条件取出的样本。

概率抽样 Probability Samples

很多时候我们需要从数据集里随机抽取数据以保证数据可靠。

  • 总体population：抽样的完整数据集
  • 概率样本Probability Samples ：在抽取该样本前，我们先计算出的元素的任何子集将进入样本的几率，该几率不一定相同，可以有权重影响等。

随机取样

其实游戏抽卡就是一种随机取样，每个非空子集都有可以量化的概率，这些概率通常不同，例如

  • 五星物品 0.60%
  • 四星 5.10%
  • 三星 94.30%
    抽卡的本质是从上述三种可能性中，按照概率进行抽样。也就是说，每次抽卡并不是等概率的选择，而是遵循一个给定的概率分布。

系统样本 A Systematic Sample

假设你有个表格，先从前10行选取随机一行，然后每隔10行选取一次，这样子获得的样本就是系统样本。

用这种方式选的每一行数据概率都是1/10，例如第21行只有在随机选取到第1行的时候才会被选取，概率为1/10。 然而该取样方式的子集只有每隔10行的集合(eg. 1,11,21,31)，每个子集有 1/10 概率被选中，但是其他子集的概率都为0(eg. 1，2，4，5…)。

放回或不放回的随机取样 Random Samples Drawn With or Without Replacement

掷骰子抛硬币都是放回的取样，总体不改变。这也是np.random.choice()的默认行为。

但是有些时候我们想要不放回的取样，例如发牌。

方便抽样 Convenience Samples (我也不知道中文翻译对没)

很多时候我们会认为我们进行的是随机抽样，但实际上是Convenience Sample。例如在街上“随机”采访，实际上我们只是选取路过的人采访而已，我们并不知道时间跨度上之后的路人路过的概率，甚至不知道总体包括的人有哪些。

经验分布 Empirical Distributions

在数据科学里，empirical和observed是同义的，所以说所谓经验分布其实就是被观察到的数据的分布情况

Table.sample()

我们之前介绍过用np.random.choice() 或者np.random.random()来从np array里面获得随机元素，或者随机选取0-1的小数。然而在Table里随机抽样需要我们随机选取行，这时我们就可以使用Table.sample():

1
2
3
Table.sample(num, with_replacement=)
#第一个参数时抽样的样本数目
#同时我们可以赋值给with_replacement=来决定是否放回抽样

The law of averages 平均定律

如果偶然的实验在相同的条件下独立重复，那么从长远来看，事件发生的频率越来越接近事件的理论概率。

样本的经验直方图

对于大型随机样本，样本的经验直方图和总体的直方图几乎一模一样。

这证明了，在统计推断中使用大型随机样本是合理的。由于大型随机样本可能类似于从中抽取的总体，从样本中计算出的数量可能接近于总体中相应的数量。

统计量 Statistic

  • 参数 Parameter: 与总体相关的数据 eg： 中位数， 平均值……
  • 统计量 Statistic： 样本中的数据 eg： 样本的中位数，平均值……

统计量的值会根据样本而改变，并非恒定。

模拟统计量的步骤：

  • 生成一个统计量
  • 重复生成多个统计量
  • 可视化结果

用Python进行随机抽样 Random Sampling in Python

  • 从Table里随机抽样：Table.sample(num, with_replacement=)
  • 从array里随机抽样：np.random.choice(array, num, replace=)
  • 从类别分布中取样

从类别分布中取样 Sampling from a Categorical Distribution

有时候我们只关心类别的取样而非具体的数字， 例如抽卡时五星，四星，三星的概率分布。

datascience的sample_proportions支持这种取样方式：

1
2
3
4
5
6
sample_proportions(num, probability array)
#第一个参数填入样本数目
#第二个参数填入各类别的概率数组
#例如如果要统计原神抽卡概率分布, 取样10000次：
sample = sample_proportions(10000, [0.006, 0.051, 0.943])
#这会返回一个np array，它的长度和传入的第二个参数相同，代表着每个类别在样本中所占比例

Reference and remark

Data 8 Text book: Inferential Thinking chapter 9-10
教科书里也介绍了基础统计学知识，这在国内高中和大学高数都有涵盖，同样国外很多学校的基础数学课程，例如Discrete mathematics和Probability theory应该也有深入学习。